Difference between revisions of "Consistent Language"
Pinventado (talk | contribs) m (Replace next line with comma) |
Sfrancisco (talk | contribs) (Updated pattern according to writing workshop comments from PLoP 2015.) |
||
| Line 13: | Line 13: | ||
}} | }} | ||
Use terms, images, notations, and other problem elements consistently throughout the learning activity. | |||
==Context== | ==Context== | ||
Students are asked to answer | Students are asked to answer problem-solving activities on an online learning system to practice a skill. They are practicing problems with the [[Try_it_yourself | Try It Yourself]] design pattern. The system also provides students with support through feedback such as [[Differentiated_feedback | Differentiated Feedback]], [[Worked_examples | Worked Examples]], and others. | ||
==Problem== | ==Problem== | ||
Students | Students are easily confused when terms, figures, or other elements of the problem or hint are used inconsistently. | ||
==Forces== | ==Forces== | ||
#'''Working memory.''' Working memory can only hold a limited amount of information | #'''Working memory.''' Working memory can only hold a limited amount of information. Adding extraneous information unnecessarily increases cognitive load required to store information<ref name="Sweller2004">Sweller, J. (2004). [http://link.springer.com/article/10.1023%2FB%3ATRUC.0000021808.72598.4d Instructional design consequences of an analogy between evolution by natural selection and human cognitive architecture]. Instructional science, 32(1-2), 9-31.</ref>. For example, using the × and symbols interchangeably to indicate multiplication will require students to remember both symbols<ref>Polya, G. (2014). [https://books.google.com/books?hl=en&lr=&id=X3xsgXjTGgoC&oi=fnd&pg=PP2&dq=How+to+Solve+It:+A+New+Aspect+of+Mathematical+Method:+A+New+Aspect+of+Mathematical+Method&ots=t6Pq_QrLr8&sig=DHb05lc8EcMqffgK60RWUSK0boQ#v=onepage&q=How%20to%20Solve%20It%3A%20A%20New%20Aspect%20of%20Mathematical%20Method%3A%20A%20New%20Aspect%20of%20Mathematical%20Method&f=false How to Solve It: A New Aspect of Mathematical Method: A New Aspect of Mathematical Method]. Princeton university press.</ref>. | ||
#'''Split-attention effect.''' Unnecessary processing of information | #'''Split-attention effect.''' Unnecessary processing of information adds cognitive load that interferes with learning<ref name="Sweller2004"/>. For example, two different figures are used in the problem statement and in the hint, but they mean the same thing. This requires the student to compare and contrast the figures before using them to make inferences. | ||
#'''Limited resources.''' Student attention and patience is a limited resource<ref>Arnold, A., Scheines, R., Beck, J.E., and Jerome, B. (2005). [http://www.aaai.org/Papers/Workshops/2005/WS-05-02/WS05-02-009.pdf Time and attention: Students, sessions, and tasks]. In Proceedings of the AAAI 2005 Workshop Educational Data Mining (pp. 62-66).</ref><ref>Bloom, B.S. (1974). [http://psycnet.apa.org/journals/amp/29/9/682/ Time and learning]. American psychologist, 29(9), 682.</ref>). Students may give up if they are overwhelmed by too many extraneous tasks they need to manage while learning. | |||
#'''Limited resources.''' Student attention and patience is a limited resource | |||
==Solution== | ==Solution== | ||
Therefore, use the same language throughout the problem. | Therefore, use the same language throughout the problem. The term [https://en.wikipedia.org/wiki/Language_(disambiguation) language] is used broadly to include different elements of the problem such as term usage, text formatting, color usage, notations, visual representations, and so forth. | ||
==Consequences== | ==Consequences== | ||
===Benefits=== | ===Benefits=== | ||
#Students | #Students need to keep track of less information in working memory. | ||
#Students do not need to spend unnecessary effort to discover the relationship between different representations used in the problem. | #Students do not need to spend unnecessary effort to discover the relationship between different representations used in the problem. | ||
# | #Straightforward tasks are easier to manage and are less likely to cause students to feel overwhelmed. | ||
===Liabilities=== | |||
<-- | #There are some cases when inconsistent problem elements are needed to introduce desirable difficulty<ref>Bjork, R.A. (1994). [http://psycnet.apa.org/psycinfo/1994-97967-009 Memory and metamemory considerations in the training of human beings]. In J. Metcalfe and A. Shimamura (Eds.), Metacognition: Knowing about knowing. (pp.185-205). Cambridge, MA: MIT Press.</ref>. For example, using a different figure in a [[Worked_example | Worked Example]]. | ||
# | #Students may not learn other representations if they are exposed to the same ones every time. | ||
# | #It is more difficult to reuse existing content because it needs to be modified to ensure that it uses a language consistent to the problem. | ||
==Evidence== | ==Evidence== | ||
| Line 51: | Line 48: | ||
===Discussion=== | ===Discussion=== | ||
Shepherds and stakeholders (i.e., data mining experts, | Shepherds, writing workshop participants, and learning system stakeholders (i.e., data mining experts, learning scientists, and educators) agreed that the problem recurs in online learning systems and the solution could properly address the problem. | ||
===Data=== | ===Data=== | ||
According to an [[Analysis:Student_affect_and_interaction_behavior_in_ASSISTments#language | analysis of ASSISTments’ data]], frustration correlated with problems that used its elements inconsistently. For example, a math problem dealing with angles used the degree notation inconsistently – “Subtract the given angle from 180°. 180 - 47 = 133.” | According to an [[Analysis:Student_affect_and_interaction_behavior_in_ASSISTments#language | analysis of ASSISTments’ data]], frustration correlated with problems that used its elements inconsistently. For example, a math problem dealing with angles used the degree notation inconsistently – “Subtract the given angle from 180°. 180 - 47 = 133.” | ||
<!--===Applied evaluation=== | <!--===Applied evaluation=== | ||
<-- Results from randomized controlled trials (RCTs) or similar tests that measures the pattern's effectiveness in an actual application. For example, compare student learning gains in an online learning system with and without applying the pattern. --> | <-- Results from randomized controlled trials (RCTs) or similar tests that measures the pattern's effectiveness in an actual application. For example, compare student learning gains in an online learning system with and without applying the pattern. --> | ||
== | ==Example== | ||
Most online learning systems adhere to instructional designs, specifically using a Consistent Language. Three notable online learning systems, which were also reported to lead to significantly better student learning, are Cognitive Tutor Algebra <ref>Koedinger, K. R., and Aleven, V. (2007). [http://link.springer.com/article/10.1007/s10648-007-9049-0 Exploring the assistance dilemma in experiments with cognitive tutors]. Educational Psychology Review, 19(3), 239-264.</ref>, Cognitive Tutor Geometry <ref>Aleven, V., Mclaren, B., Roll, I., and Koedinger, K. (2006). [http://content.iospress.com/articles/international-journal-of-artificial-intelligence-in-education/jai16-2-02 Toward meta-cognitive tutoring: A model of help seeking with a Cognitive Tutor]. International Journal of Artificial Intelligence in Education, 16(2), 101-128.</ref> and ASSISTMents (Heffernan and Heffernan 2014). | |||
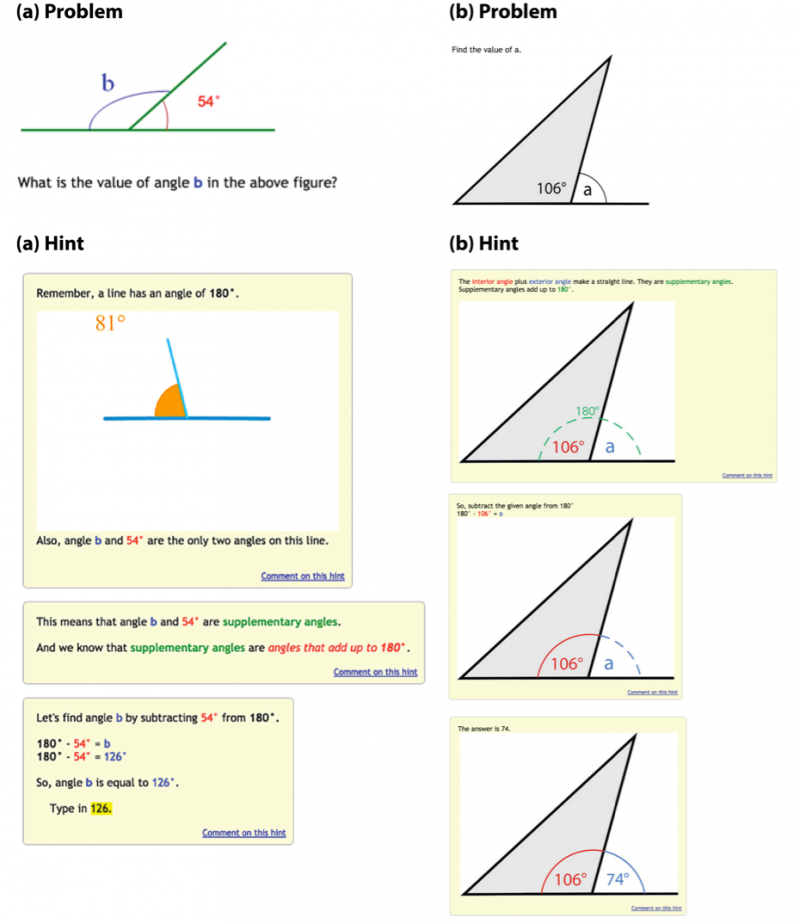
Figure a shows an example of a problem and its corresponding hints with an inconsistent language. The hint uses a different figure, orientation, and color to represent the angle. Students will need to analyze the hint and relate it to the problem before it can be used to make inferences. Figure b shows an example of a problem and its corresponding hints that uses a consistent figure. It will probably take students less time to process, understand, and utilize these hints to make inferences. | |||
[[File:Consistent_language_ex.png | center|800px]] | [[File:Consistent_language_ex.png | center|800px]] | ||
==Related patterns== | |||
Use the [[Familiar_language | Familiar Language]] design pattern when selecting the representation for creating a [[Consistent_language | Consistent Language]] to facilitate understanding . It is good practice to use a [[Consistent_language | Consistent Language]] to develop any type of content in an online learning system. | |||
Revision as of 06:36, 12 April 2016
| Consistent Language | |
| Contributors | Paul Inventado, Peter Scupelli |
|---|---|
| Last modification | April 12, 2016 |
| Source | {{{source}}} |
| Pattern formats | OPR Alexandrian |
| Usability | |
| Learning domain | General |
| Stakeholders | Teachers Students |
| Production | |
| Data analysis | Student affect and interaction behavior in ASSISTments |
| Confidence | |
| Evaluation | PLoP 2015 writing workshop Talk:ASSISTments |
| Application | ASSISTments |
| Applied evaluation | ASSISTments |
Use terms, images, notations, and other problem elements consistently throughout the learning activity.
Context
Students are asked to answer problem-solving activities on an online learning system to practice a skill. They are practicing problems with the Try It Yourself design pattern. The system also provides students with support through feedback such as Differentiated Feedback, Worked Examples, and others.
Problem
Students are easily confused when terms, figures, or other elements of the problem or hint are used inconsistently.
Forces
- Working memory. Working memory can only hold a limited amount of information. Adding extraneous information unnecessarily increases cognitive load required to store information[1]. For example, using the × and symbols interchangeably to indicate multiplication will require students to remember both symbols[2].
- Split-attention effect. Unnecessary processing of information adds cognitive load that interferes with learning[1]. For example, two different figures are used in the problem statement and in the hint, but they mean the same thing. This requires the student to compare and contrast the figures before using them to make inferences.
- Limited resources. Student attention and patience is a limited resource[3][4]). Students may give up if they are overwhelmed by too many extraneous tasks they need to manage while learning.
Solution
Therefore, use the same language throughout the problem. The term language is used broadly to include different elements of the problem such as term usage, text formatting, color usage, notations, visual representations, and so forth.
Consequences
Benefits
- Students need to keep track of less information in working memory.
- Students do not need to spend unnecessary effort to discover the relationship between different representations used in the problem.
- Straightforward tasks are easier to manage and are less likely to cause students to feel overwhelmed.
Liabilities
- There are some cases when inconsistent problem elements are needed to introduce desirable difficulty[5]. For example, using a different figure in a Worked Example.
- Students may not learn other representations if they are exposed to the same ones every time.
- It is more difficult to reuse existing content because it needs to be modified to ensure that it uses a language consistent to the problem.
Evidence
Literature
Peterson and Peterson[6] found that unfamiliar combinations of letters could only be held in memory for a few seconds. In a different study, Miller[7] indicated that working memory could only hold five to nine chunks of unfamiliar information at a time. Learners are more likely to perform better when working memory is not overloaded by unnecessary information[1].
Discussion
Shepherds, writing workshop participants, and learning system stakeholders (i.e., data mining experts, learning scientists, and educators) agreed that the problem recurs in online learning systems and the solution could properly address the problem.
Data
According to an analysis of ASSISTments’ data, frustration correlated with problems that used its elements inconsistently. For example, a math problem dealing with angles used the degree notation inconsistently – “Subtract the given angle from 180°. 180 - 47 = 133.”
Example
Most online learning systems adhere to instructional designs, specifically using a Consistent Language. Three notable online learning systems, which were also reported to lead to significantly better student learning, are Cognitive Tutor Algebra [8], Cognitive Tutor Geometry [9] and ASSISTMents (Heffernan and Heffernan 2014).
Figure a shows an example of a problem and its corresponding hints with an inconsistent language. The hint uses a different figure, orientation, and color to represent the angle. Students will need to analyze the hint and relate it to the problem before it can be used to make inferences. Figure b shows an example of a problem and its corresponding hints that uses a consistent figure. It will probably take students less time to process, understand, and utilize these hints to make inferences.
Related patterns
Use the Familiar Language design pattern when selecting the representation for creating a Consistent Language to facilitate understanding . It is good practice to use a Consistent Language to develop any type of content in an online learning system.
References
- ↑ 1.0 1.1 1.2 Sweller, J. (2004). Instructional design consequences of an analogy between evolution by natural selection and human cognitive architecture. Instructional science, 32(1-2), 9-31.
- ↑ Polya, G. (2014). How to Solve It: A New Aspect of Mathematical Method: A New Aspect of Mathematical Method. Princeton university press.
- ↑ Arnold, A., Scheines, R., Beck, J.E., and Jerome, B. (2005). Time and attention: Students, sessions, and tasks. In Proceedings of the AAAI 2005 Workshop Educational Data Mining (pp. 62-66).
- ↑ Bloom, B.S. (1974). Time and learning. American psychologist, 29(9), 682.
- ↑ Bjork, R.A. (1994). Memory and metamemory considerations in the training of human beings. In J. Metcalfe and A. Shimamura (Eds.), Metacognition: Knowing about knowing. (pp.185-205). Cambridge, MA: MIT Press.
- ↑ Peterson, L. and Peterson, M. (1959). Short-term retention of individual verbal items. Journal of Experimental Psychology 58: 193–198.
- ↑ Miller, G.A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review 63: 81–97.
- ↑ Koedinger, K. R., and Aleven, V. (2007). Exploring the assistance dilemma in experiments with cognitive tutors. Educational Psychology Review, 19(3), 239-264.
- ↑ Aleven, V., Mclaren, B., Roll, I., and Koedinger, K. (2006). Toward meta-cognitive tutoring: A model of help seeking with a Cognitive Tutor. International Journal of Artificial Intelligence in Education, 16(2), 101-128.